Week1

Two Sum

  • Array

Problem

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in any order.

Example 1:

1
2
3

Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Example 2:

1
2

Input: nums = [3,2,4], target = 6
Output: [1,2]

Example 3:

1
2

Input: nums = [3,3], target = 6
Output: [0,1]

Constraints:

  • 2 <= nums.length <= 104
  • 109 <= nums[i] <= 109
  • 109 <= target <= 109
  • Only one valid answer exists.

Follow-up: Can you come up with an algorithm that is less than O(n2) time complexity?

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56


from collections import defaultdict

class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        # # Let's try a simple solution first
        # # O(n^2) - Time, O(1) - space
        # for i, first in enumerate(nums):
        #     for j, second in enumerate(nums):
        #         if i == j: continue
        #         if first + second == target:
        #             return [i, j]

        ## Two pass hash map
        ## O(n^2) - Time, O(n) space
        # data = defaultdict(list)
        # for i, x in enumerate(nums):
        #     data[x].append(i)
        # for k, v in data.items():
        #     chk_s = target - k
        #     diff = data.get(chk_s)
        #     if diff:
        #         if len(diff) > 1:
        #             return [diff[0], diff[1]]
        #         else:
        #             if chk_s != k:
        #                 return [v[0], data[chk_s][0]]

        ## Cleaner hashmap solution
        ## Two pass hashmap
        ## O(n) - time , O(n) - space

        # data = {}
        # for i, x in enumerate(nums):
        #     data[x] = i

        # for i, x in enumerate(nums):
        #     diff = target - x
        #     if diff in data and i != data[diff]:
        #         return [i, data[diff]]

        ## Cleaner hashmap solution
        ## One pass hashmap
        ## O(n) - time , O(n) - space

        data = {}
        for i, x in enumerate(nums):
            diff = target - x
            if diff in data:
                return [i, data[diff]]
            data[x] = i

Valid Parentheses

Problem

  • Stack

Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.

An input string is valid if:

  1. Open brackets must be closed by the same type of brackets.
  2. Open brackets must be closed in the correct order.
  3. Every close bracket has a corresponding open bracket of the same type.

Example 1:

1
2

Input: s = "()"
Output: true

Example 2:

1
2

Input: s = "()[]{}"
Output: true

Example 3:

1
2

Input: s = "(]"
Output: false

Constraints:

  • 1 <= s.length <= 104
  • s consists of parentheses only '()[]{}'.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        
        stack = list()
        for brac in s:
            if stack:
                if brac == ")" and stack[-1] == "(":
                    stack.pop()
                elif brac == "}" and stack[-1] == "{":
                    stack.pop()
                elif brac == "]" and stack[-1] == "[":
                    stack.pop()
                else:
                    stack.append(brac)
            else:
                stack.append(brac)

        if stack:
            return False
        else:
            return True

Merge Two Sorted Lists

  • Linked List

Problem

You are given the heads of two sorted linked lists list1 and list2.

Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists.

Return the head of the merged linked list.

1
2

Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]

Example 2:

1
2

Input: list1 = [], list2 = []
Output: []

Example 3:

1
2

Input: list1 = [], list2 = [0]
Output: [0]

Constraints:

  • The number of nodes in both lists is in the range [0, 50].
  • 100 <= Node.val <= 100
  • Both list1 and list2 are sorted in non-decreasing order.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

# Definition for singly-linked list.
class ListNode(object):
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class Solution(object):
    def mergeTwoLists(self, list1, list2):
        """
        :type list1: Optional[ListNode]
        :type list2: Optional[ListNode]
        :rtype: Optional[ListNode]
        """
        idx1 = 0
        idx2 = 0
        merged_ll = None
        start = None
        while True:

            if list1 == None and list2 == None:
                break
            
            if merged_ll is None:
                start = merged_ll = ListNode()
            else:
                merged_ll.next = ListNode()
                merged_ll = merged_ll.next

            if list1 != None and list2 != None:
                if list1.val < list2.val:
                    merged_ll.val = list1.val
                    list1 = list1.next
                else:
                    merged_ll.val = list2.val
                    list2 = list2.next
            elif list1 == None:
                merged_ll.val = list2.val
                list2 = list2.next
            else:
                merged_ll.val = list1.val
                list1 = list1.next

        return start

Best Time to Buy and Sell Stock

  • Array

Problem

You are given an array prices where prices[i] is the price of a given stock on the ith day.

You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.

Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.

Example 1:

1
2
3
4

Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

Example 2:

1
2
3

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.

Constraints:

  • 1 <= prices.length <= 10^5
  • 0 <= prices[i] <= 10^4

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        ## O(n^2) don't pass
        # max_profit = 0
        # for i, x in enumerate(prices):
        #     for y in prices[i:]:
        #         max_profit = max(max_profit, y-x)

        # return int(max_profit)

        # O(n) - time , O(1) - space
        price = prices[0]
        max_profit = 0

        for x in prices:
            if x < price:
                price = x
                continue
            potential_profit = x - price
            if potential_profit > max_profit:
                max_profit = potential_profit
            
        return max_profit

Valid Palindrome

Problem

A phrase is a palindrome if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.

Given a string s, return true if it is a palindrome, or false otherwise.

Example 1:

1
2
3

Input: s = "A man, a plan, a canal: Panama"
Output: true
Explanation: "amanaplanacanalpanama" is a palindrome.

Example 2:

1
2
3

Input: s = "race a car"
Output: false
Explanation: "raceacar" is not a palindrome.

Example 3:

1
2
3
4

Input: s = " "
Output: true
Explanation: s is an empty string "" after removing non-alphanumeric characters.
Since an empty string reads the same forward and backward, it is a palindrome.

Constraints:

  • 1 <= s.length <= 2 * 10^5
  • s consists only of printable ASCII characters.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution(object):
    def isPalindrome(self, s):
        """
        :type s: str
        :rtype: bool
        """
        # Fast and accepted
        # s = s.lower()
        # s = [x for x in s if x.isalnum()]
        # # print(s)
        # len_s = len(s)
        # for i in range(len_s//2):
        #     if s[i] == s[-i-1]:
        #         continue
        #     else:
        #         return False

        # return True

        # Faster
        s = s.lower()
        s = [x for x in s if x.isalnum()]
        len_s = len(s)
        return all (s[i] == s[-i-1] for i in range(len_s//2))

Invert Binary Tree

Problem

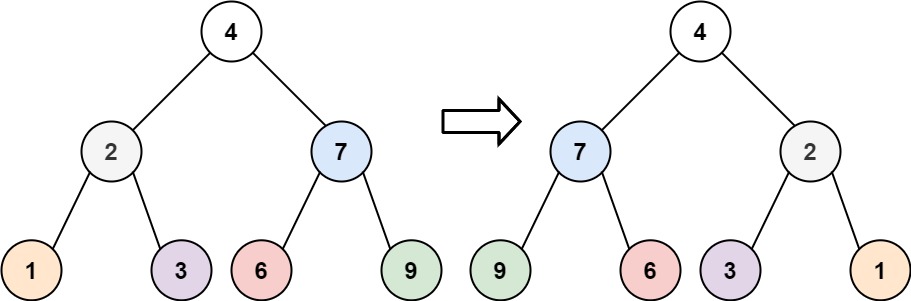
Given the root of a binary tree, invert the tree, and return its root.

Example 1:

https://assets.leetcode.com/uploads/2021/03/14/invert1-tree.jpg

1
2

Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

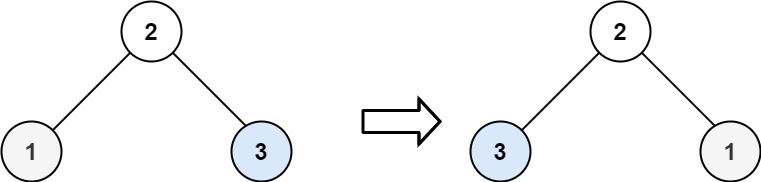
Example 2:

https://assets.leetcode.com/uploads/2021/03/14/invert2-tree.jpg

1
2

Input: root = [2,1,3]
Output: [2,3,1]

Example 3:

1
2

Input: root = []
Output: []

Constraints:

  • The number of nodes in the tree is in the range [0, 100].
  • 100 <= Node.val <= 100

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def build_binary_tree(root):
		"""
		create a binary tree from array
		root: array
		"""
    tot_nodes = len(root)
    tree_nodes = []
    for i in range(tot_nodes):
        tree_nodes.append(TreeNode(val=root[i]))

    for i in range(tot_nodes//2):
        tree_nodes[i].left = tree_nodes[i*2+1]
        tree_nodes[i].right = tree_nodes[i*2+2]

    return tree_nodes[0]

def traverse_binary_tree(root):
		"""
		Traverse a binary tree
		root: TreeNode
		"""
    
    bt_arr = []
    stack = [root]
    while stack:
        
        node = stack.pop(0)
        
        bt_arr.append(node.val)
        if node.left:
            stack.append(node.left)
        if node.right:
            stack.append(node.right)

    return bt_arr

class Solution(object):

    def invertTree(self, root):
        """
        :type root: TreeNode
        :rtype: TreeNode
        """
        stack = [root]
        while stack:
            node = stack.pop(0)
            if node:
                if node.left:
                    stack.append(node.left)
                if node.right:
                    stack.append(node.right)

                node.left, node.right = node.right, node.left

        return root

Valid Anagram

Problem

Given two strings s and t, return true if t is an anagram of s, and false otherwise.

An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the vaoriginal letters exactly once.

Example 1:

1
2

Input: s = "anagram", t = "nagaram"
Output: true

Example 2:

1
2

Input: s = "rat", t = "car"
Output: false

Constraints:

  • 1 <= s.length, t.length <= 5 * 10^4
  • s and t consist of lowercase English letters.

Follow up: What if the inputs contain Unicode characters? How would you adapt your solution to such a case?

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

from collections import Counter
class Solution:
    def isAnagram(self, s: str, t: str) -> bool:
        count_s = Counter(s)
        count_t = Counter(t)

        if len(count_s.keys()) != len(count_t.keys()):
            return False        

        for k, v in count_s.items():
            try:
                if count_s[k] == count_t[k]:
                    continue
                else:
                    return False
            except KeyError as e:
                return False
        
        return True

Problem

Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

1
2
3

Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4

Example 2:

1
2
3

Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1

Constraints:

  • 1 <= nums.length <= 10^4
  • -10^4 < nums[i], target < 10^4
  • All the integers in nums are unique.
  • nums is sorted in ascending order.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

from typing import List

class Solution:
    def search(self, nums: List[int], target: int) -> int:
				# O(log(N)) solution
        start, end = 0, len(nums)-1
        while start <= end:
						# this prevents memory issues if numbers are too big
            mid = start + (end-start)//2
            
            if target == nums[mid]:
                return mid

            elif target <= nums[mid]:
                end = mid-1
            else:
                start = mid+1
        return -1

Flood Fill

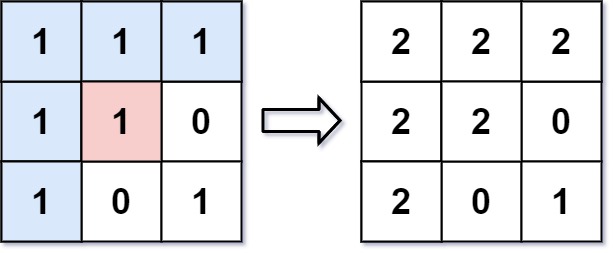
An image is represented by an m x n integer grid image where image[i][j] represents the pixel value of the image.

You are also given three integers sr, sc, and color. You should perform a flood fill on the image starting from the pixel image[sr][sc].

To perform a flood fill, consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, plus any pixels connected 4-directionally to those pixels (also with the same color), and so on. Replace the color of all of the aforementioned pixels with color.

Return the modified image after performing the flood fill.

https://assets.leetcode.com/uploads/2021/06/01/flood1-grid.jpg

1
2
3
4

Input: image = [[1,1,1],[1,1,0],[1,0,1]], sr = 1, sc = 1, color = 2
Output: [[2,2,2],[2,2,0],[2,0,1]]
Explanation: From the center of the image with position (sr, sc) = (1, 1) (i.e., the red pixel), all pixels connected by a path of the same color as the starting pixel (i.e., the blue pixels) are colored with the new color.
Note the bottom corner is not colored 2, because it is not 4-directionally connected to the starting pixel.

Example 2:

1
2
3

Input: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, color = 0
Output: [[0,0,0],[0,0,0]]
Explanation: The starting pixel is already colored 0, so no changes are made to the image.

Constraints:

  • m == image.length
  • n == image[i].length
  • 1 <= m, n <= 50
  • 0 <= image[i][j], color < 2^16
  • 0 <= sr < m
  • 0 <= sc < n

10. Lowest Common Ancestor of a Binary Search Tree

Problem

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

https://assets.leetcode.com/uploads/2018/12/14/binarysearchtree_improved.png

1
2
3

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

https://assets.leetcode.com/uploads/2018/12/14/binarysearchtree_improved.png

1
2
3

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

1
2

Input: root = [2,1], p = 2, q = 1
Output: 2

Constraints:

  • The number of nodes in the tree is in the range [2, 105].
  • 109 <= Node.val <= 10^9
  • All Node.val are unique.
  • p != q
  • p and q will exist in the BST.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

from typing import List

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:

    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:

        while root:
            # if root is higher than both p and q, then the lowest ancestor
            # must be on the left side of the root and vice versa
            if root.val > p.val and root.val > q.val:
                root = root.left
            elif root.val < p.val and root.val < q.val:
                root = root.right     
            else:
                return root

Instead of BST, the following code finds out LCA if the tree is Binary Tree

(Lowest Common Ancestor of a Binary Tree)

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112

from typing import List

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
        self.parent = None
        self.level = 0

class Solution:

    def build_tree(self, nodes = []) -> TreeNode:
        tot_nodes = len(nodes)
        tree_nodes = []
        for i in range(tot_nodes):
            tree_nodes.append(TreeNode(x=nodes[i]))

        for i in range(tot_nodes//2):
            tree_nodes[i].left = tree_nodes[i*2+1]
            tree_nodes[i].right = tree_nodes[i*2+2]

        return tree_nodes[0]

    def traverse_binary_tree(self, root):
    
        bt_arr = []
        stack = [root]
        while stack:
            
            node = stack.pop(0)
            
            bt_arr.append(node.val)
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)

        return bt_arr

    def search(self, root: TreeNode, tgt: TreeNode) -> TreeNode:
        stack = [root]
        while stack:
            node = stack.pop(0)
            if node:
                if node.val == tgt.val:
                    return node
                if node.left:
                    node.left.parent = node
                    stack.append(node.left)
                if node.right:
                    node.right.parent = node
                    stack.append(node.right)

    def backtrace_root(self, tgt: TreeNode)-> List:
        path = []
        path = [tgt]
        while tgt:
            path.append(tgt.parent)
            tgt = tgt.parent
        return path

    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:

        head = root
        root.parent = None
        root.level = 0
        stack = [root]
        level = 0
        # Add parents to tree
        while stack:
            
            node = stack.pop(0)
            if node:
                level+=1
                if node.left:
                    node.left.parent = node
                    node.left.level = level
                    stack.append(node.left)
                if node.right:
                    node.right.parent = node
                    node.right.level = level
                    stack.append(node.right)

        path_p = self.backtrace_root(p)
        path_q = self.backtrace_root(q)
        # print([x.val for x in path_p ])
        # print([x.val for x in path_q if x])
        # print(path_p, path_q)
        
        common_nodes = set(path_p).intersection(set(path_q))
        common_nodes.remove(None)
        common_nodes = list(common_nodes)
        common_nodes = sorted(common_nodes, key=lambda x: x.level)
        return common_nodes[-1]
                

if __name__ == "__main__":
    p = TreeNode(x=2)
    q = TreeNode(x=4)
    # nodes = [6,2,8,0,4,7,9,"null","null",3,5]
    nodes = [6,2,8,0,4,7,9,"null","null",3,5]
    obj = Solution()
    root = obj.build_tree(nodes)
    print(obj.traverse_binary_tree(root))
    print(root.val, root.parent)
    p = obj.search(root=root, tgt=p)
    q = obj.search(root=root, tgt=q)
    print(p.val, p.parent, p.left, p.right)
    print(q.val, q.parent, q.left, q.right)
    print(obj.lowestCommonAncestor(root, p, q).val)

Balanced Binary Tree

Linked List Cycle

Implement Queue using Stacks

References

  1. Grind 75 - A better Blind 75 you can customize, by the author of Blind 75